This page is for an old version of Hexaly Optimizer. We recommend that you update your version and read the documentation for the latest stable release.

Black-Box Optimization

Caution

If the function isn’t computationally expensive and could be evaluated thousands of times during the solution process, using a black-box function may not be the best option. Consider using LocalSolver with an external function.

Note

Note that this functionality is not available in the LSP language.

Note

While the black-box API is integrated in LocalSolver’s API, only a select handful of operators currently support the black-box optimization process: bool, integer and float variables, as well as constants and black-box functions.

In this section we detail how to optimize a black-box function in each programming language supported by LocalSolver (C++, Java, .NET, Python). To illustrate this description we will minimize the Branin function through a black-box interface. The number of evaluations will be limited to 20.

The Branin function is defined by f(x) = a(x2 - b*x1² + c*x1 - r)² + s(1-t)cos(x1) + s with a=1, b=5.1/(4π²), c=5/π, s=10 and t=1/(8π). The domains of x1 and x2 are respectively [-5,10] and [0,15].

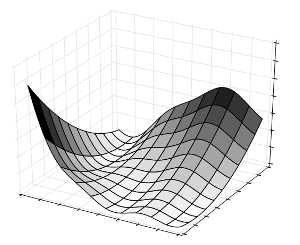
../_images/branin.png

For more details, see branin.html

Black-Box optimization in Python

In Python, a black-function is simply a function or a method passed to LocalSolver. This method must take a single parameter of type LSBlackBoxArgumentValues. The method uses this object to access the decision values of the current point to evaluate and returns the value of the function at this point:

def branin_eval(args):
    x = args[0]
    y = args[1]
    return math.pow(y - (5.1 / (4.0 * math.pi * math.pi)) * x * x
        + 5.0 / math.pi * x - 6, 2)
        + 10 * (1 - 1 / (8.0 * math.pi)) * math.cos(x) + 10

A LocalSolver model is then created to optimize this black-box function. The function is transformed into a LSExpression using the method LSModel.double_blackbox_function(). The decisions are associated with the function using a LSExpression of type CALL. Via the LSBlackBoxContext, the solver is then told to perform 20 evaluations of the function. This context can also be used to provide bounds for the function. The solution value can be obtained after the resolution using the LSSolution:

with localsolver.LocalSolver() as ls:
   model = ls.model
   x = model.float(-5, 10)
   y = model.float(0, 15)
   f = model.double_blackbox_function(branin_eval)
   call = model.call()
   call.add_operand(f)
   call.add_operand(x)
   call.add_operand(y)
   model.minimize(call)
   model.close()

   f.blackbox_context.set_evaluation_limit(20)
   ls.solve()

   sol = ls.solution
   print("x = {}".format(sol.get_value(x)))
   print("y = {}".format(sol.get_value(y)))
   print("obj = {}".format(sol.get_value(call)))

Black-Box optimization in C++

In C++, a black-box function is passed to LocalSolver as an object implementing the interface LSBlackBoxFunction. This interface has a single virtual method call taking as parameter an object of type LSBlackBoxArgumentValues. The call method uses this object to access the decision values of the current point to evaluate and returns the value of the function at this point:

#include <iostream>
#include "localsolver.h"

#define PI 3.14159

class Branin : public LSBlackBoxFunction<lsdouble> {
    lsdouble call(const LSBlackBoxArgumentValues& args) override {
        lsdouble x = args.getDoubleValue(0);
        lsdouble y = args.getDoubleValue(1);
        return pow(y - (5.1 / (4.0 * PI * PI)) * x * x + 5.0 / PI * x - 6, 2)
            + 10 * (1 - 1 / (8.0 * PI)) * cos(x) + 10;
    }
};

A LocalSolver model is then created to optimize this black-box function. The black-box function is transformed into a LSExpression using the method LSModel::blackBoxFunction(). The decisions are associated to the function using a LSExpression of type O_Call. Via the LSBlackBoxContext, the solver is then told to perform 20 evaluations the function. This context can also be used to provide bounds for the function. The solution value can be obtained after the resolution using the LSSolution:

int main(){
    Branin braninFunction;

    LocalSolver ls;
    LSModel model = ls.getModel();

    LSExpression x = model.floatVar(-5,10);
    LSExpression y = model.floatVar(0,15);
    LSExpression f = model.blackBoxFunction(&braninFunction);
    LSExpression call = model.call();
    call.addOperand(f);
    call.addOperand(x);
    call.addOperand(y);
    model.minimize(call);
    model.close();

    f.getBlackBoxContext().setEvaluationLimit(20);
    ls.solve();

    LSSolution sol = ls.getSolution();
    std::cout << "x = " << sol.getDoubleValue(x) << std::endl;
    std::cout << "y = " << sol.getDoubleValue(y) << std::endl;
    std::cout << "obj = " << sol.getDoubleValue(call) << std::endl;
}

Black-Box optimization in .NET

In .NET, a black-box function is passed to LocalSolver as a delegate method taking as a single parameter an object of type LSBlackBoxArgumentValues. The method uses this object to access the decision values of the current point to evaluate and returns the value of the function at this point. In the example we use a static method:

public static double BraninEval(LSBlackBoxArgumentValues args) {
    double x = args.GetDoubleValue(0);
    double y = args.GetDoubleValue(1);

    return Math.Pow(y - (5.1 / (4.0 * Math.PI * Math.PI)) * x * x
        + 5.0 / Math.PI * x - 6, 2)
        + 10 * (1 - 1 / (8.0 * Math.PI)) * Math.Cos(x) + 10;
}

A LocalSolver model is then created to optimize this black-box function. The black-box function is transformed into a LSExpression using the method :meth:DoubleBlackBoxFunction. The decisions are associated to the function using an LSExpression of type Call. Via LSBlackBoxContext, the solver is then told to perform 20 evaluations of the function. This context can also be used to provide bounds for the function. The solution value can be obtained after the resolution using the LSSolution:

public static void Main(string[] args)
{
    LocalSolver ls = new LocalSolver();
    LSModel model = ls.GetModel();
    LSExpression x = model.Float(-5,10);
    LSExpression y = model.Float(0,15);
    LSExpression f = model.DoubleBlackBoxFunction(BraninEval);
    LSExpression call = model.Call();
    call.AddOperand(f);
    call.AddOperand(x);
    call.AddOperand(y);
    model.Minimize(call);
    model.Close();

    f.GetBlackBoxContext().SetEvaluationLimit(20);
    ls.Solve();

    LSSolution sol = ls.GetSolution();
    Console.WriteLine("x = "+sol.GetDoubleValue(x));
    Console.WriteLine("y = "+sol.GetDoubleValue(y));
    Console.WriteLine("obj = "+sol.GetDoubleValue(call));
}

Black-Box optimization in Java

In Java, a black-box function is passed to LocalSolver as an object implementing the interface LSDoubleBlackBoxFunction. This interface has a single method call taking as parameter an object of type LSBlackBoxArgumentValues. The call method uses this object to access the decision values of the current point to evaluate and returns the value of the function at this point.

A LocalSolver model is then created to optimize this black-box function. The black-box function is transformed into an LSExpression using the doubleBlackBoxFunction method. The decisions are associated to the function using an LSExpression of type Call. Via the LSBlackBoxContext, the solver is then told to perform 20 evaluations of the black-box function. This context can also be used to provide bounds for the function. The solution value can be obtained after the resolution using the LSSolution:

import localsolver.*;

public class Branin {
    public static void main(String [] args) {

        LocalSolver ls = new LocalSolver();
        LSModel model = ls.getModel();
        LSExpression f = model.doubleBlackBoxFunction(new LSDoubleBlackBoxFunction(){
        public double call(LSBlackBoxArgumentValues args){
            double x = args.getDoubleValue(0);
            double y = args.getDoubleValue(1);
            return Math.pow(y - (5.1 / (4.0 * Math.PI * Math.PI)) * x * x
                + 5.0 / Math.PI * x - 6, 2)
                + 10 * (1 - 1 / (8.0 * Math.PI)) * Math.cos(x) + 10;
        }
        });

        LSExpression x = model.floatVar(-5,10);
        LSExpression y = model.floatVar(0,15);
        LSExpression call = model.call();
        call.addOperand(f);
        call.addOperand(x);
        call.addOperand(y);
        model.minimize(call);
        model.close();

        f.getBlackBoxContext().setEvaluationLimit(20);
        ls.solve();

        LSBBSolution solution = ls.getSolution();
        System.out.println("x = " + solution.getDoubleValue(x));
        System.out.println("y = " + solution.getDoubleValue(y));
        System.out.println("obj = " + solution.getDoubleValue(call));
    }
}