JobShop¶
Principles learned¶
- Add multiple list decision variables
- Constrain the number of elements in a list
- Order numeric decision variables by pairing them up with a list variable
Problem¶
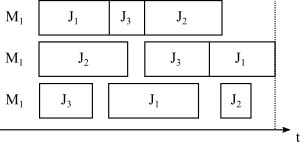
A set of jobs has to be processed on every machine of the shop. Each job consists in an ordered sequence of tasks (called activities), each representing the processing of the job on one of the machines. Each job has one activity per machine, and cannot start an activity while the previous activity of the job is not completed. Each activity has a given processing time and each machine can only process one activity at a time.
The goal is to find a sequence of jobs that minimizes the makespan: the time when all jobs have been processed.
Download the exampleData¶
The instances provided follow the Taillard format. The format of the data files is as follows:
- First line: number of jobs, number of machines, seed used to generate the instance, upper and lower bound previously found.
- For each job: the processing time on each machine (given in the processing order).
- For each job: the processing order (ordered list of visited machines).
Program¶
We use integer decision variables to model the start times of the activities. The end time expressions are deduced by summing the start time and the processing time of each activity.
The precedence constraints are easily written: for each job, any activity of this job must start after the activity processed by the previous machine has ended.
In addition to the integer decisions representing the start times of the activities, we also use list decision variables. As in the Flowshop example, a list models the ordering of activities within a machine. We constrain all the jobs to be processed on each machine thanks to the “count” operator.
The disjunctive resource constraints — each machine can only process one activity at a time — can be reformulated as follows: given a sequence of jobs, the activity corresponding to any job must start after the activity corresponding to the previous job has ended.
To model these constraints, we pair up the integer decisions (the start times) with the list decisions (the job orderings). We write a lambda function, expressing the relationship between the start times of two consecutive activities. This function is used within an “and” operator over all activities processed by a machine.
The makespan to minimize is the time when all the activities have been processed.
- Execution:
- localsolver jobshop.lsp inFileName=instances/ft10.txt [outFileName=] [lsTimeLimit=]
/********** jobshop.lsp **********/
use io;
// The input files follow the "Taillard" format
function input() {
local usage = "Usage: localsolver jobshop.lsp inFileName=instanceFile [outFileName=outputFile] [lsTimeLimit=timeLimit]";
if (inFileName == nil) throw usage;
inFile = io.openRead(inFileName);
inFile.readln();
nbJobs = inFile.readInt();
nbMachines = inFile.readInt();
inFile.readln();
inFile.readln();
// Processing times for each job on each machine (given in the processing order)
for [j in 0..nbJobs-1][k in 0..nbMachines-1] {
processingTimesInProcessingOrder[j][k] = inFile.readInt();
k += 1;
}
inFile.readln();
for [j in 0..nbJobs-1][k in 0..nbMachines-1] {
local m = inFile.readInt() - 1;
// Processing order of machines for each job
machineOrder[j][k] = m;
// Reorder processing times: processingTime[j][m] is the processing time of the
// activity of job j that is processed on machine m
processingTime[j][m] = processingTimesInProcessingOrder[j][k];
}
inFile.close();
// Trivial upper bound for the start times of the activities
maxStart = sum[j in 0..nbJobs-1][m in 0..nbMachines-1] (processingTime[j][m]);
}
function model() {
// Integer decisions: start time of each activity
// start[j][m] is the start time of the activity of job j which is processed on machine m
start[j in 0..nbJobs-1][m in 0..nbMachines-1] <- int(0, maxStart);
end[j in 0..nbJobs-1][m in 0..nbMachines-1] <- start[j][m] + processingTime[j][m];
// Precedence constraints between the activities of a job
for [j in 0..nbJobs-1][k in 1..nbMachines-1]
constraint start[j][machineOrder[j][k]] >= end[j][machineOrder[j][k-1]];
// Sequence of activities on each machine
jobsOrder[m in 0..nbMachines-1] <- list(nbJobs);
for [m in 0..nbMachines-1] {
// Each job has an activity scheduled on each machine
constraint count(jobsOrder[m]) == nbJobs;
// Disjunctive resource constraints between the activities on a machine
constraint and(0..nbJobs-2, i => start[jobsOrder[m][i+1]][m] >= end[jobsOrder[m][i]][m]);
}
// Minimize the makespan: end of the last activity of the last job
makespan <- max[j in 0..nbJobs-1] (end[j][machineOrder[j][nbMachines-1]]);
minimize makespan;
}
// Parameterizes the solver
function param() {
if (lsTimeLimit == nil) lsTimeLimit = 60;
}
// Writes the solution in a file with the following format:
// - for each machine, the job sequence
function output() {
if (outFileName != nil) {
outFile = io.openWrite(outFileName);
println("Solution written in file ", outFileName);
for [m in 0..nbMachines-1]
outFile.println[j in 0..nbJobs-1](jobsOrder[m].value[j], " ");
}
}
- Execution (Windows)
- set PYTHONPATH=%LS_HOME%\bin\python jobshop.py instances\ft10.txt
- Execution (Linux)
- export PYTHONPATH=/opt/localsolver_9_5/bin/python jobshop.py instances/ft10.txt
########## jobshop.py ##########
import localsolver
import sys
# The input files follow the "Taillard" format
def read_instance(filename):
with open(filename) as f:
lines = f.readlines()
first_line = lines[1].split()
# Number of jobs
nb_jobs = int(first_line[0])
# Number of machines
nb_machines = int(first_line[1])
# Processing times for each job on each machine (given in the processing order)
processing_times_in_processing_order = [[int(lines[i].split()[j]) for j in range(nb_machines)] for i in range(3, 3+nb_jobs)]
# Processing order of machines for each job
machine_order = [[int(lines[i].split()[j])-1 for j in range(nb_machines)] for i in range(4+nb_jobs, 4+2*nb_jobs)]
# Reorder processing times: processing_time[j][m] is the processing time of the
# activity of job j that is processed on machine m
processing_time = [[processing_times_in_processing_order[j][machine_order[j].index(m)] for m in range(nb_machines)] for j in range(nb_jobs)]
# Trivial upper bound for the start times of the activities
max_start = sum(sum(processing_time[j]) for j in range(nb_jobs))
return (nb_jobs, nb_machines, processing_time, machine_order, max_start)
def main(instance_file, output_file, time_limit):
nb_jobs, nb_machines, processing_time, machine_order, max_start = read_instance(instance_file)
with localsolver.LocalSolver() as ls:
# Declares the optimization model
model = ls.model
# Integer decisions: start time of each activity
# start[j][m] is the start time of the activity of job j which is processed on machine m
start = [[model.int(0, max_start) for m in range(nb_machines)] for j in range(nb_jobs)]
end = [[start[j][m] + processing_time[j][m] for m in range(nb_machines)] for j in range(nb_jobs)]
start_array = model.array(start)
end_array = model.array(end)
# Precedence constraints between the activities of a job
for j in range(nb_jobs):
for k in range(1, nb_machines):
model.constraint(start[j][machine_order[j][k]] >= end[j][machine_order[j][k-1]])
# Sequence of activities on each machine
jobs_order = [model.list(nb_jobs) for m in range(nb_machines)]
for m in range(nb_machines):
# Each job has an activity scheduled on each machine
sequence = jobs_order[m]
model.constraint(model.eq(model.count(sequence), nb_jobs))
# Disjunctive resource constraints between the activities on a machine
sequence_selector = model.lambda_function(lambda i: model.geq(model.at(start_array, sequence[i], m), model.at(end_array, sequence[i-1], m)))
model.constraint(model.and_(model.range(1, nb_jobs), sequence_selector))
# Minimize the makespan: end of the last activity of the last job
makespan = model.max([end[j][machine_order[j][nb_machines-1]] for j in range(nb_jobs)])
model.minimize(makespan)
model.close()
# Parameterizes the solver
ls.param.time_limit = time_limit
ls.solve()
# Writes the solution in a file with the following format:
# - for each machine, the job sequence
if output_file != None:
final_jobs_order = [list(jobs_order[m].value) for m in range(nb_machines)]
with open(output_file, "w") as f:
print("Solution written in file", output_file)
for m in range(nb_machines):
for j in range(nb_jobs):
f.write(str(final_jobs_order[m][j]) + " ")
f.write("\n")
if __name__ == '__main__':
if len(sys.argv) < 2:
print("Usage: python jobshop.py instance_file [output_file] [time_limit]")
sys.exit(1)
instance_file = sys.argv[1]
output_file = sys.argv[2] if len(sys.argv) >= 3 else None
time_limit = int(sys.argv[3]) if len(sys.argv) >= 4 else 60
main(instance_file, output_file, time_limit)
- Compilation / Execution (Windows)
- cl /EHsc jobshop.cpp -I%LS_HOME%\include /link %LS_HOME%\bin\localsolver95.libjobshop instances\ft10.txt
- Compilation / Execution (Linux)
- g++ jobshop.cpp -I/opt/localsolver_9_5/include -llocalsolver95 -lpthread -o jobshop./jobshop instances/ft10.txt
/********** jobshop.cpp **********/
#include <iostream>
#include <fstream>
#include <vector>
#include <limits>
#include <numeric>
#include <algorithm>
#include "localsolver.h"
using namespace localsolver;
class Jobshop {
private:
// Number of jobs
int nbJobs;
// Number of machines
int nbMachines;
// Processing order of machines for each job
std::vector<std::vector<int> > machineOrder;
// Processing time on each machine for each job (given in the machine order)
std::vector<std::vector<int> > processingTime;
// Trivial upper bound for the start times of the activities
int maxStart;
// LocalSolver
LocalSolver localsolver;
// Decision variables: start times of the activities
std::vector<std::vector<LSExpression> > start;
// Decision variables: sequence of activities on each machine
std::vector<LSExpression> jobsOrder;
// Objective = minimize the makespan: end of the last activity of the last job
LSExpression makespan;
// The input files follow the "Taillard" format
void readInstance(const std::string& fileName) {
std::ifstream infile;
infile.exceptions(std::ifstream::failbit | std::ifstream::badbit);
infile.open(fileName.c_str());
infile.ignore(std::numeric_limits<std::streamsize>::max(), '\n');
infile >> nbJobs;
infile >> nbMachines;
infile.ignore(std::numeric_limits<std::streamsize>::max(), '\n');
// Processing times for each job on each machine (given in the processing order)
infile.ignore(std::numeric_limits<std::streamsize>::max(), '\n');
std::vector<std::vector<int> > processingTimesInProcessingOrder
= std::vector<std::vector<int> >(nbJobs, std::vector<int>(nbMachines));
for (int j = 0; j < nbJobs; j++) {
for (int m = 0; m < nbMachines; m++) {
infile >> processingTimesInProcessingOrder[j][m];
}
}
// Processing order of machines for each job
infile.ignore(std::numeric_limits<std::streamsize>::max(), '\n');
infile.ignore(std::numeric_limits<std::streamsize>::max(), '\n');
machineOrder.resize(nbJobs);
for (int j = 0; j < nbJobs; j++) {
machineOrder[j].resize(nbMachines);
for (int m = 0; m < nbMachines; m++) {
int x;
infile >> x;
machineOrder[j][m] = x - 1;
}
}
// Reorder processing times: processingTime[j][m] is the processing time of the
// activity of job j that is processed on machine m
for (int j = 0; j < nbJobs; j++) {
processingTime.resize(nbJobs);
for (int m = 0; m < nbMachines; m++) {
processingTime[j].resize(nbMachines);
std::vector<int>::iterator findM = std::find(machineOrder[j].begin(),
machineOrder[j].end(), m);
unsigned int k = std::distance(machineOrder[j].begin(), findM);
processingTime[j][m] = processingTimesInProcessingOrder[j][k];
}
}
// Trivial upper bound for the start times of the activities
maxStart = 0;
for (int j = 0; j < nbJobs; j++)
maxStart += std::accumulate(processingTime[j].begin(), processingTime[j].end(), 0);
infile.close();
}
public:
Jobshop(const std::string& fileName) : localsolver() {
readInstance(fileName);
}
void solve(int timeLimit) {
// Declares the optimization model
LSModel model = localsolver.getModel();
// Integer decisions: start time of each activity
start.resize(nbJobs);
std::vector<std::vector<LSExpression> > end(nbJobs);
for (unsigned int j = 0; j < nbJobs; j++) {
start[j].resize(nbMachines);
end[j].resize(nbMachines);
for (unsigned int m = 0; m < nbMachines; m++) {
start[j][m] = model.intVar(0, maxStart);
end[j][m] = start[j][m] + processingTime[j][m];
}
}
LSExpression startArray = model.array();
LSExpression endArray = model.array();
for (int j = 0; j < nbJobs; j++) {
startArray.addOperand(model.array(start[j].begin(), start[j].end()));
endArray.addOperand(model.array(end[j].begin(), end[j].end()));
}
// Precedence constraints between the activities of a job
for (int j = 0; j < nbJobs; j++) {
for (int k = 1; k < nbMachines; k++) {
model.constraint(start[j][machineOrder[j][k]] >= end[j][machineOrder[j][k-1]]);
}
}
// Sequence of activities on each machine
jobsOrder.resize(nbMachines);
for (int m = 0; m < nbMachines; m++) {
jobsOrder[m] = model.listVar(nbJobs);
}
for (int m = 0; m < nbMachines; m++) {
// Each job has an activity scheduled on each machine
LSExpression sequence = jobsOrder[m];
model.constraint(model.eq(model.count(sequence), nbJobs));
// Disjunctive resource constraints between the activities on a machine
LSExpression sequenceSelector = model.createLambdaFunction([&](LSExpression i) {
return model.geq(model.at(startArray, sequence[i], m),
model.at(endArray, sequence[i-1], m));
});
model.constraint(model.and_(model.range(1, nbJobs), sequenceSelector));
}
// Minimize the makespan: end of the last activity of the last job
makespan = model.max();
for (int j = 0; j < nbJobs; j++) {
makespan.addOperand(end[j][machineOrder[j][nbMachines-1]]);
}
model.minimize(makespan);
model.close();
// Parameterizes the solver
localsolver.getParam().setTimeLimit(timeLimit);
localsolver.solve();
}
// Writes the solution in a file with the following format:
// - for each machine, the job sequence
void writeSolution(const std::string& fileName) {
std::ofstream outfile(fileName.c_str());
if (!outfile.is_open()) {
std::cerr << "File " << fileName << " cannot be opened." << std::endl;
exit(1);
}
std::cout << "Solution written in file " << fileName << std::endl;
for (int m = 0; m < nbMachines; m++) {
LSCollection finalJobsOrder = jobsOrder[m].getCollectionValue();
for (int j = 0; j < nbJobs; j++) {
outfile << finalJobsOrder.get(j) << " ";
}
outfile << std::endl;
}
outfile.close();
}
};
int main(int argc, char** argv) {
if (argc < 2) {
std::cout << "Usage: jobshop instanceFile [outputFile] [timeLimit]" << std::endl;
exit(1);
}
const char* instanceFile = argv[1];
const char* outputFile = argc > 2 ? argv[2] : NULL;
const char* strTimeLimit = argc > 3 ? argv[3] : "60";
Jobshop model(instanceFile);
try {
const int timeLimit = atoi(strTimeLimit);
model.solve(timeLimit);
if (outputFile != NULL) model.writeSolution(outputFile);
return 0;
} catch (const std::exception& e) {
std::cerr << "An error occurred: " << e.what() << std::endl;
return 1;
}
}
- Compilation / Execution (Windows)
- copy %LS_HOME%\bin\localsolvernet.dll .csc Jobshop.cs /reference:localsolvernet.dlljobshop instances\ft10.txt
/********** JobShop.cs **********/
using System;
using System.IO;
using localsolver;
public class Jobshop : IDisposable
{
// Number of jobs
private int nbJobs;
// Number of machines
private int nbMachines;
// Processing time on each machine for each job (given in the machine order)
private long[,] processingTime;
// Processing order of machines for each job
private int[,] machineOrder;
// Trivial upper bound for the start times of the activities
private long maxStart;
// LocalSolver
private LocalSolver localsolver;
// Decision variables: start times of the activities
private LSExpression[,] start;
// Decision variables: sequence of activities on each machine
private LSExpression[] jobsOrder;
// Objective = minimize the makespan: end of the last activity of the last job
private LSExpression makespan;
public Jobshop(string fileName)
{
localsolver = new LocalSolver();
ReadInstance(fileName);
}
// The input files follow the "Taillard" format
private void ReadInstance(string fileName)
{
using (StreamReader input = new StreamReader(fileName))
{
input.ReadLine();
string[] splitted = input.ReadLine().Split(' ');
nbJobs = int.Parse(splitted[0]);
nbMachines = int.Parse(splitted[1]);
// Processing times for each job on each machine (given in the processing order)
input.ReadLine();
long[,] processingTimesInProcessingOrder = new long[nbJobs, nbMachines];
for (int j = 0; j < nbJobs; j++)
{
splitted = input.ReadLine().Trim().Split(' ');
for (int m = 0; m < nbMachines; m++)
{
processingTimesInProcessingOrder[j, m] = long.Parse(splitted[m]);
}
}
// Processing order of machines for each job
input.ReadLine();
machineOrder = new int[nbJobs, nbMachines];
for (int j = 0; j < nbJobs; j++)
{
splitted = input.ReadLine().Trim().Split(' ');
for (int m = 0; m < nbMachines; m++)
{
machineOrder[j, m] = int.Parse(splitted[m]) - 1;
}
}
// Reorder processing times: processingTime[j, m] is the processing time of the
// activity of job j that is processed on machine m
processingTime = new long[nbJobs, nbMachines];
// Trivial upper bound for the start times of the activities
maxStart = 0;
for (int j = 0; j < nbJobs; j++)
{
for (int m = 0; m < nbMachines; m++)
{
int machineIndex = nbMachines;
for (int k = 0; k < nbMachines; k++)
{
if (machineOrder[j, k] == m) {
machineIndex = k;
break;
}
}
processingTime[j, m] = processingTimesInProcessingOrder[j, machineIndex];
maxStart += processingTime[j, m];
}
}
}
}
public void Dispose()
{
localsolver.Dispose();
}
public void Solve(int timeLimit)
{
// Declares the optimization model
LSModel model = localsolver.GetModel();
// Integer decisions: start time of each activity
// start[j, m] is the start time of the activity of job j which is processed on machine m
start = new LSExpression[nbJobs, nbMachines];
LSExpression[,] end = new LSExpression[nbJobs, nbMachines];
for (int j = 0; j < nbJobs; j++)
{
for (int m = 0; m < nbMachines; m++)
{
start[j, m] = model.Int(0, maxStart);
end[j, m] = start[j, m] + processingTime[j, m];
}
}
LSExpression startArray = model.Array(start);
LSExpression endArray = model.Array(end);
// Precedence constraints between the activities of a job
for (int j = 0; j < nbJobs; j++)
{
for (int k = 1; k < nbMachines; k++)
{
model.Constraint(start[j, machineOrder[j, k]] >= end[j, machineOrder[j, k-1]]);
}
}
// Sequence of activities on each machine
jobsOrder = new LSExpression[nbMachines];
for (int m = 0; m < nbMachines; m++)
{
jobsOrder[m] = model.List(nbJobs);
}
for (int m = 0; m < nbMachines; m++)
{
// Each job has an activity scheduled on each machine
LSExpression sequence = jobsOrder[m];
model.Constraint(model.Count(sequence) == nbJobs);
// Disjunctive resource constraints between the activities on a machine
LSExpression sequenceSelector = model.LambdaFunction(i => startArray[sequence[i], m]
>= endArray[sequence[i-1], m]);
model.Constraint(model.And(model.Range(1, nbJobs), sequenceSelector));
}
// Minimize the makespan: end of the last activity of the last job
makespan = model.Max();
for (int j = 0; j < nbJobs; j++)
{
makespan.AddOperand(end[j, machineOrder[j, nbMachines-1]]);
}
model.Minimize(makespan);
model.Close();
// Parameterizes the solver
localsolver.GetParam().SetTimeLimit(timeLimit);
localsolver.Solve();
}
// Writes the solution in a file with the following format:
// - for each machine, the job sequence
public void WriteSolution(string fileName)
{
using (StreamWriter output = new StreamWriter(fileName)) {
Console.WriteLine("Solution written in file " + fileName);
for (int m = 0; m < nbMachines; m++)
{
LSCollection finalJobsOrder = jobsOrder[m].GetCollectionValue();
for (int i = 0; i < nbJobs; i++)
{
int j = (int) finalJobsOrder.Get(i);
output.Write(j + " ");
}
output.WriteLine();
}
}
}
public static void Main(string[] args)
{
if (args.Length < 1)
{
Console.WriteLine ("Usage: Jobshop instanceFile [outputFile] [timeLimit]");
System.Environment.Exit(1);
}
string instanceFile = args [0];
string outputFile = args.Length > 1 ? args[1] : null;
string strTimeLimit = args.Length > 2 ? args[2] : "60";
using (Jobshop model = new Jobshop(instanceFile))
{
model.Solve (int.Parse(strTimeLimit));
if (outputFile != null)
model.WriteSolution(outputFile);
}
}
}
- Compilation / Execution (Windows)
- javac Jobshop.java -cp %LS_HOME%\bin\localsolver.jarjava -cp %LS_HOME%\bin\localsolver.jar;. jobshop instances\ft10.txt
- Compilation / Execution (Linux)
- javac Jobshop.java -cp /opt/localsolver_9_5/bin/localsolver.jarjava -cp /opt/localsolver_9_5/bin/localsolver.jar:. jobshop instances/ft10.txt
/********** Jobshop.java **********/
import java.util.*;
import java.io.*;
import localsolver.*;
public class Jobshop {
// Number of jobs
private int nbJobs;
// Number of machines
private int nbMachines;
// Processing time on each machine for each job (given in the machine order)
private long[][] processingTime;
// Processing order of machines for each job
private int[][] machineOrder;
// Trivial upper bound for the start times of the activities
private long maxStart;
// LocalSolver
final LocalSolver localsolver;
// Decision variables: start times of the activities
private LSExpression[][] start;
// Decision variables: sequence of activities on each machine
private LSExpression[] jobsOrder;
// Objective = minimize the makespan: end of the last activity of the last job
private LSExpression makespan;
public Jobshop(LocalSolver localsolver, String fileName) throws IOException {
this.localsolver = localsolver;
readInstance(fileName);
}
// The input files follow the "Taillard" format
private void readInstance(String fileName) throws IOException {
try (Scanner input = new Scanner(new File(fileName))) {
input.nextLine();
nbJobs = input.nextInt();
nbMachines = input.nextInt();
input.nextLine();
input.nextLine();
// Processing times for each job on each machine (given in the processing order)
long[][] processingTimesInProcessingOrder = new long[nbJobs][nbMachines];
for (int j = 0; j < nbJobs; j++) {
for (int m = 0; m < nbMachines; m++) {
processingTimesInProcessingOrder[j][m] = input.nextInt();
}
}
// Processing order of machines for each job
input.nextLine();
input.nextLine();
machineOrder = new int[nbJobs][nbMachines];
for (int j = 0; j < nbJobs; j++) {
for (int m = 0; m < nbMachines; m++) {
machineOrder[j][m] = input.nextInt() - 1;
}
}
// Reorder processing times: processingTime[j][m] is the processing time of the
// activity of job j that is processed on machine m
processingTime = new long[nbJobs][nbMachines];
// Trivial upper bound for the start times of the activities
maxStart = 0;
for (int j = 0; j < nbJobs; j++) {
for (int m = 0; m < nbMachines; m++) {
int machineIndex = nbMachines;
for (int k = 0; k < nbMachines; k++) {
if (machineOrder[j][k] == m) {
machineIndex = k;
break;
}
}
processingTime[j][m] = processingTimesInProcessingOrder[j][machineIndex];
maxStart += processingTime[j][m];
}
}
}
}
public void solve(int timeLimit) {
// Declares the optimization model
LSModel model = localsolver.getModel();
// Integer decisions: start time of each activity
// start[j][m] is the start time of the activity of job j which is processed on machine m
start = new LSExpression[nbJobs][nbMachines];
LSExpression[][] end = new LSExpression[nbJobs][nbMachines];
for (int j = 0; j < nbJobs; j++) {
for (int m = 0; m < nbMachines; m++) {
start[j][m] = model.intVar(0, maxStart);
end[j][m] = model.sum(start[j][m], processingTime[j][m]);
}
}
LSExpression startArray = model.array(start);
LSExpression endArray = model.array(end);
// Precedence constraints between the activities of a job
for (int j = 0; j < nbJobs; j++) {
for (int k = 1; k < nbMachines; k++) {
model.constraint(model.geq(start[j][machineOrder[j][k]],
end[j][machineOrder[j][k-1]]));
}
}
// Sequence of activities on each machine
jobsOrder = new LSExpression[nbMachines];
for (int m = 0; m < nbMachines; m++) {
jobsOrder[m] = model.listVar(nbJobs);
}
for (int m = 0; m < nbMachines; m++) {
// Each job has an activity scheduled on each machine
LSExpression sequence = jobsOrder[m];
model.constraint(model.eq(model.count(sequence), nbJobs));
// Disjunctive resource constraints between the activities on a machine
LSExpression mExpr = model.createConstant(m);
LSExpression sequenceSelector = model.lambdaFunction(i -> model.geq(
model.at(startArray, model.at(sequence, i), mExpr),
model.at(endArray, model.at(sequence, model.sub(i, 1)), mExpr)));
model.constraint(model.and(model.range(1, nbJobs), sequenceSelector));
}
// Minimize the makespan: end of the last activity of the last job
makespan = model.max();
for (int j = 0; j < nbJobs; j++) {
makespan.addOperand(end[j][machineOrder[j][nbMachines-1]]);
}
model.minimize(makespan);
model.close();
// Parameterizes the solver
localsolver.getParam().setTimeLimit(timeLimit);
localsolver.solve();
}
// Writes the solution in a file with the following format:
// - for each machine, the job sequence
public void writeSolution(String fileName) throws IOException {
try (PrintWriter output = new PrintWriter(fileName)) {
System.out.println("Solution written in file " + fileName);
for (int m = 0; m < nbMachines; m++) {
LSCollection finalJobsOrder = jobsOrder[m].getCollectionValue();
for (int i = 0; i < nbJobs; i++) {
int j = Math.toIntExact(finalJobsOrder.get(i));
output.write(j + " ");
}
output.write("\n");
}
}
}
public static void main(String[] args) {
if (args.length < 1) {
System.out.println("Usage: java Jobshop instanceFile [outputFile] [timeLimit]");
System.exit(1);
}
String instanceFile = args[0];
String outputFile = args.length > 1 ? args[1] : null;
String strTimeLimit = args.length > 2 ? args[2] : "60";
try (LocalSolver localsolver = new LocalSolver()) {
Jobshop model = new Jobshop(localsolver, instanceFile);
model.solve(Integer.parseInt(strTimeLimit));
if (outputFile != null) {
model.writeSolution(outputFile);
}
} catch (Exception ex) {
System.err.println(ex);
ex.printStackTrace();
System.exit(1);
}
}
}
