Branin function¶

Principles learned¶

Add float decision variables
Minimize a non-linear objective

Create a highly non-linear expression: with operators “cos” and “pow”

Problem¶

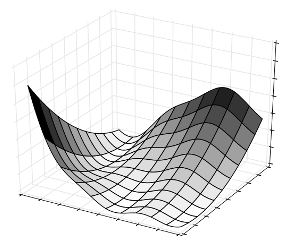
Branin function is defined by f(x) = a(x2 - b*x1² + c*x1 - r)² + s(1-t)cos(x1) + s

For more details, see : branin.html

Download the example

Program¶

Constants are fixed to the recommended values: a=1, b=5.1/(4π²), c=5/π, s=10 and t=1/(8π). The domains of x1 and x2 are respectively [-5,10] and [0,15].

The model is really straightforward: two decision variables x1 and x2 are declared, and then the Branin function to be minimized is applied to this couple.

LSP
Python
C++
C#
Java

Execution:: localsolver branin.lsp [lsTimeLimit=] [solFileName=]

/********** branin.lsp **********/

use io;

/* Declares the optimization model. */
function model() {
    PI = 3.14159265359;
    a = 1;
    b = 5.1/(4*pow(PI,2));
    c = 5/PI;
    r = 6;
    s = 10;
    t = 1/(8*PI);

    x1 <- float(-5,10);
    x2 <- float(0,15);

    // f = a(x2 - b*x1^2 + c*x1 - r)^2 + s(1-t)cos(x1) + s
    f <- a*pow(x2 - b*pow(x1, 2) + c*x1 - r, 2) + s*(1-t)*cos(x1) + s;

    minimize f;
}

/* Parameterizes the solver. */
function param() {
    if(lsTimeLimit == nil) lsTimeLimit = 6;
}

/* Writes the solution in a file */
function output() {
    if (solFileName != nil) // write solution file if needed
    {
        local solFile = io.openWrite(solFileName);
        solFile.println("x1=", x1.value);
        solFile.println("x2=", x2.value);
    }
}

Execution (Windows): set PYTHONPATH=%LS_HOME%\bin\python27\

python branin.py

Execution (Linux): export PYTHONPATH=/opt/localsolver_XXX/bin/python27/

python branin.py

########## branin.py ##########

import localsolver
import sys

with localsolver.LocalSolver() as ls:

    # Parameters of the function
    PI = 3.14159265359
    a = 1;
    b = 5.1/(4*pow(PI,2));
    c = 5/PI;
    r = 6;
    s = 10;
    t = 1/(8*PI);

    #
    # Declares the optimization model
    #
    model = ls.model

    # Numerical decisions
    x1 = model.float(-5.0,10.0)
    x2 = model.float(0.0,15.0)

    # f = a(x2 - b*x1^2 + c*x1 - r)^2 + s(1-t)cos(x1) + s
    f = a*(x2 - b*x1**2 + c*x1 -r)**2 + s*(1-t)*model.cos(x1) + s

    # Minimize f
    model.minimize(f)

    model.close()

    #
    # Parameterizes the solver
    #
    ls.param.nb_threads = 2
    if len(sys.argv) >= 3: ls.create_phase().time_limit = int(sys.argv[2])
    else: ls.create_phase().time_limit = 6

    ls.solve()

    #
    # Writes the solution in a file
    #
    if len(sys.argv) >= 2:
        with open(sys.argv[1], 'w') as f:
            f.write("x1=%f\n" % x1.value)
            f.write("x2=%f\n" % x2.value)

Compilation / Execution (Windows): cl /EHsc branin.cpp -I%LS_HOME%\include /link %LS_HOME%\bin\localsolver.dll.lib

branin

Compilation / Execution (Linux): g++ branin.cpp -I/opt/localsolver_XXX/include -llocalsolver -lpthread -o branin

branin

//********* branin.cpp *********

#include <iostream>
#include <fstream>
#include <vector>
#include "localsolver.h"

using namespace localsolver;
using namespace std;

class Branin {
public:
    // Solver
    LocalSolver localsolver;

    // LS Program variables.
    LSExpression x1;
    LSExpression x2;

    void solve(int limit) {
        // Parameters of the function
        lsdouble PI = 3.14159265359;
        lsdouble a = 1;
        lsdouble b = 5.1/(4*pow(PI, 2.0));
        lsdouble c = 5/PI;
        lsdouble r = 6;
        lsdouble s = 10;
        lsdouble t = 1/(8*PI);

        // Declares the optimization model. 
        LSModel model = localsolver.getModel();

        // Numerical decisions
        x1 = model.floatVar(-5.0, 10.0);
        x2 = model.floatVar(0.0, 15.0);

        // f = a(x2 - b*x1^2 + c*x1 - r)^2 + s(1-t)cos(x1) + s
        LSExpression f = a*model.pow(x2 - b*model.pow(x1, 2) + c*x1 - r, 2) + s*(1-t)*model.cos(x1) + s;

        // Minimize f
        model.minimize(f);
        model.close();

        // Parameterizes the solver. 
        LSPhase phase = localsolver.createPhase();
        phase.setTimeLimit(limit);

        localsolver.solve();
    }

    // Writes the solution in a file
    void writeSolution(const string& fileName){
        ofstream outfile;
        outfile.exceptions(ofstream::failbit | ofstream::badbit);
        outfile.open(fileName.c_str());
        outfile << "x1=" << x1.getDoubleValue() << endl;
        outfile << "x2=" << x2.getDoubleValue() << endl;
    }
};

int main(int argc, char** argv){
    const char* solFile = argc > 1 ? argv[1] : NULL;
    const char* strTimeLimit = argc > 2 ? argv[2] : "6";    

    try {
        Branin model;
        model.solve(atoi(strTimeLimit));
        if(solFile != NULL) model.writeSolution(solFile);
    } catch (const exception& e){
        cerr << "Error occurred: " << e.what() << endl;
        return 1;
    }
    return 0;
}

Compilation/Execution (Windows): copy %LS_HOME%\bin\*net.dll .

csc Branin.cs /reference:localsolvernet.dll

Branin

/********** Branin.cs **********/

using System;
using System.IO;
using localsolver;

public class Branin : IDisposable
{
    // Solver
    private LocalSolver localsolver;

    // LS Program variables
    private LSExpression x1;
    private LSExpression x2;

    public Branin()
    {
        localsolver = new LocalSolver();
    }

    public void Dispose()
    {
        if(localsolver != null)
            localsolver.Dispose();
    }

    public void Solve(int limit)
    {
        // Parameters of the function
        double PI = 3.14159265359;
        double a = 1;
        double b = 5.1 / (4 * Math.Pow(PI, 2.0));
        double c = 5 / PI;
        double r = 6;
        double s = 10;
        double t = 1 / (8 * PI);

        // Declares the optimization model
        LSModel model = localsolver.GetModel();

        // Numerical decisions
        x1 = model.Float(-5, 10);
        x2 = model.Float(0, 15);

        // f = a(x2 - b*x1^2 + c*x1 - r)^2 + s(1-t)cos(x1) + s
        LSExpression f = a * model.Pow(x2 - b * model.Pow(x1, 2) + c * x1 - r, 2) + s * (1 - t) * model.Cos(x1) + s;

        // Minimize f
        model.Minimize(f);
        model.Close();

        // Parameterizes the solver.
        LSPhase phase = localsolver.CreatePhase();
        phase.SetTimeLimit(limit);

        localsolver.Solve();
    }

    // Writes the solution in a file
    public void WriteSolution(string fileName)
    {
        using (StreamWriter output = new StreamWriter(fileName))
        {
            output.WriteLine("x1=" + x1.GetDoubleValue());
            output.WriteLine("x2=" + x2.GetDoubleValue());
        }
    }

    public static void Main(string[] args)
    {
        string outputFile = args.Length > 0 ? args[0] : null;
        string strTimeLimit = args.Length > 1 ? args[1] : "6";

        using (Branin model = new Branin())
        {
            model.Solve(int.Parse(strTimeLimit));
            if (outputFile != null)
                model.WriteSolution(outputFile);
        }
    }
}

Compilation / Execution (Windows): javac Branin.java -cp %LS_HOME%\bin\localsolver.jar

java -cp %LS_HOME%\bin\localsolver.jar;. Branin

Compilation/Execution (Linux): javac Branin.java -cp /opt/localsolver_XXX/bin/localsolver.jar

java -cp /opt/localsolver_XXX/bin/localsolver.jar:. Branin

/********** Branin.java **********/

import java.io.*;
import localsolver.*;

public class Branin {
	// Parameters of the function
	private static final double PI = 3.14159265359;
	private static final int a = 1;
	private static final double b = 5.1 / (4 * Math.pow(PI, 2));
	private static final double c = 5 / PI;
	private static final int r = 6;
	private static final int s = 10;
	private static final double t = 1 / (8 * PI);

	// Solver
	private LocalSolver localsolver;

	// LS Program variables.
	private LSExpression x1;
	private LSExpression x2;

	// Declares the optimization model.
	private void solve(int limit) {
		localsolver = new LocalSolver();
		LSModel model = localsolver.getModel();

		// numerical decisions
		x1 = model.floatVar(-5, 10);
		x2 = model.floatVar(0, 15);

		// f = a(x2 - b*x1^2 + c*x1 - r)^2 + s(1-t)cos(x1) + s
		LSExpression f = model.sum();

		// f1 = x2 - b*x1^2 + c*x1 - r
		LSExpression f1 = model.sum();
		f1.addOperand(x2);
		f1.addOperand(model.prod(-b, model.pow(x1, 2)));
		f1.addOperand(model.prod(c, x1));
		f1.addOperand(-r);

		// f = a*f1^2 + s(1-t)cos(x1) + s
		f.addOperand(model.prod(a, model.pow(f1, 2)));
		f.addOperand(model.prod(s * (1 - t), model.cos(x1)));
		f.addOperand(s);

		// minimize f
		model.minimize(f);

		// close model, then solve
		model.close();

		// Parameterizes the solver.
		LSPhase phase = localsolver.createPhase();
		phase.setTimeLimit(limit);

		localsolver.solve();
	}

	// Writes the solution in a file
	private void writeSolution(String fileName) throws IOException {
		try (PrintWriter output = new PrintWriter(fileName)) {
			output.println("x1=" + x1.getDoubleValue());
			output.println("x2=" + x2.getDoubleValue());
		}
	}

	public static void main(String[] args) {
		String outputFile = args.length > 0 ? args[0] : null;
		String strTimeLimit = args.length > 1 ? args[1] : "6";

		try {
			Branin model = new Branin();
			model.solve(Integer.parseInt(strTimeLimit));
			if (outputFile != null) {
				model.writeSolution(outputFile);
			}
		} catch (Exception ex) {
			System.err.println(ex);
			ex.printStackTrace();
			System.exit(1);
		}
	}
}