Quadratic assignment problem¶
Principles learned¶
- Define the actual set of decision variables
- Add a list decision variable
- Access the list elements with an “at” operator
- Constrain the number of elements in the list with operator “count”
- Access a multi-dimensional array with an “at” operator
- Get the value of a list variable
Problem¶
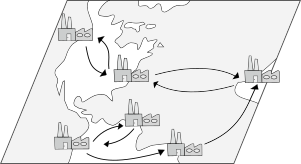
The Quadratic Assignment Problem (QAP) is a fundamental combinatorial optimization problem in the branch of optimization and operations research. It originally comes from facility location applications and models the following real-life problem. There are a set of n facilities and a set of n locations. For each pair of locations, a distance is specified and for each pair of facilities a weight or flow is specified (e.g., the amount of supplies transported between the two facilities). The problem is to assign all facilities to different locations with the goal of minimizing the sum of the distances multiplied by the corresponding flows. Intuitively, the cost function encourages factories with high flows between each other to be placed close together. The problem statement resembles that of the assignment problem, except that the cost function is expressed in terms of quadratic inequalities, hence the name. For more details, we invite the reader to have a look to the QAPLIB webpage.
Download the exampleData¶
Instance files are from the QAPLIB.
The format of the data is as follows:
- Number of points
- Matrix A: distance between each location
- Matrix B: flow between each facility
Program¶
The initial idea for the model is really straightforward, as there is no need to linearize thanks to LocalSolver’s non-linear operators:
- Decisions are booleans
x[f][l]which are equal to 1 if facility f is assigned to the location l. - Facilities are constrained to be on one location
- Locations are constrained to receive only one facility
This leads to the following model:
x[f in 1..nbFacilities][l in 1..nbLocations] <- bool();
for[f in 1..nbFacilities]
constraint sum[l in 1..nbLocations](x[f][l]) == 1;
for[l in 1..nbLocations]
constraint sum[f in 1..nbFacilities](x[f][l]) == 1;
The quadratic objective could simply be declared as the sum of products of flow and distance as follows:
obj <- sum[f1 in 1..nbFacilities][f2 in 1..nbFacilities]
[l1 in 1..nbLocations][l2 in 1..nbLocations]
(A[l1][l2] * B[f1][f2] * x[f1][l1] * x[f2][l2]);
However, it could create O(n^4) expressions (depending on the sparsity of matrix B). The large number of expressions created would slow down the number of iterations per second - thus the overall performance - and instances with more than a few hundred variables would quickly become intractable (instances with 80 points tai80a and tai80b already take around 8GB of memory).
What we actually want as the objective is the sum, for each pair of locations (l1,l2), of the product between the distance between l1 and l2 and the flow between the factory on l1 and the factory on l2. It is possible to do just that in LocalSolver thanks to “at” operators that can retrieve a member of an array indexed by an expression (see this page for more information about the “at” operator). First, we retrieve the ID of the factory on each location as shown below:
facilityOnLocations[l in 0..nbLocations-1] <- sum[f in 0..nbFacilities-1](f*x[f][l]);
Then, the objective is naturally written as follows:
obj <- sum[l1 in 0..nbLocations-1][l2 in 0..nbLocations-1]
(A[l1][l2] * B[facilityOnLocations[l1]][facilityOnLocations[l2]]);
The objective now only creates O(n^2) expressions. Instances with thousands of points can be tackled with no resource issues.
In the end, we have just created by hand the concept of permutation: given a
permutation p of numbers in [0..n-1], p(l) is the ID of the factory on
location l. Thus, we can write an even more compact model by using the
list variables provided by LocalSolver.
The only constraint is for the list to contain all the facilities and the
objective is the same as above. You will find below the model using a list
variable for each language. The downloadable archive also contains models with
binary variables.
- Execution:
- localsolver qap.lsp inFileName=instances/esc32a.dat [lsTimeLimit=] [solFileName=]
/********** qap.lsp **********/
use io;
/* Reads instance data */
function input(){
local usage = "Usage : localsolver qap.lsp "
+ "inFileName=inName [solFileName=solName] [lsTimeLimit=limit]";
if(inFileName == nil) throw usage;
local inFile = io.openRead(inFileName);
n = inFile.readInt();
// Distance between locations
A[0..n-1][0..n-1] = inFile.readInt();
// Flow between facilites (indices of the map must start at 0
// to access it with an "at" operator")
B[0..n-1][0..n-1] = inFile.readInt();
}
/* Declares the optimization model */
function model() {
// Permutation such that p[i] is the facility on the location i
p <- list(n);
// The list must be complete
constraint count(p) == n;
// Minimize the sum of product distance*flow
obj <- sum[i in 0..n-1][j in 0..n-1]( A[i][j] * B[p[i]][p[j]]);
minimize obj;
}
/* Parameterizes the solver. */
function param() {
if(lsTimeLimit == nil) lsTimeLimit = 300;
}
/* Writes the solution in a file with the following format:
* - n objValue
* - permutation p */
function output() {
if (solFileName == nil) return;
local solFile = io.openWrite(solFileName);
solFile.println(n + " " + obj.value);
for[i in 0..n-1]{
solFile.print(p.value[i] + " ");
}
solFile.println();
}
- Execution (Windows)
- set PYTHONPATH=%LS_HOME%\bin\python27\python qap.py instances\esc32a.dat
- Execution (Linux)
- export PYTHONPATH=/opt/localsolver_XXX/bin/python27/python qap.py instances/esc32a.dat
########## qap.py ##########
import localsolver
import sys
if len(sys.argv) < 2:
print ("Usage: python qap.py inputFile [outputFile] [timeLimit]")
sys.exit(1)
def read_integers(filename):
with open(filename) as f:
return [int(elem) for elem in f.read().split()]
with localsolver.LocalSolver() as ls:
#
# Reads instance data
#
file_it = iter(read_integers(sys.argv[1]))
# Number of points
n = file_it.next()
# Distance between locations
A = [[file_it.next() for j in range(n)] for i in range(n)]
# Flow between factories
B = [[file_it.next() for j in range(n)] for i in range(n)]
#
# Declares the optimization model
#
model = ls.model
# Permutation such that p[i] is the facility on the location i
p = model.list(n)
# The list must be complete
model.constraint(model.eq(model.count(p), n));
# Create B as an array to be accessed by an at operator
array_B = model.array(model.array(B[i]) for i in range(n))
# Minimize the sum of product distance*flow
obj = model.sum(A[i][j]*model.at(array_B, p[i], p[j]) for j in range(n) for i in range(n));
model.minimize(obj)
model.close()
#
# Parameterizes the solver
#
if len(sys.argv) >= 4: ls.create_phase().time_limit = int(sys.argv[3])
else: ls.create_phase().time_limit = 300
ls.solve()
#
# Writes the solution in a file with the following format:
# - n objValue
# - permutation p
#
if len(sys.argv) >= 3:
with open(sys.argv[2], 'w') as outfile:
outfile.write("%d %d\n" % (n, obj.value))
for i in range(n):
outfile.write("%d " % p.value[i])
outfile.write("\n")
- Compilation / Execution (Windows)
- cl /EHsc qap.cpp -I%LS_HOME%\include /link %LS_HOME%\bin\localsolver.dll.libqap instances\esc32a.dat
- Compilation / Execution (Linux)
- g++ qap.cpp -I/opt/localsolver_XXX/include -llocalsolver -lpthread -o qap./qap instances/esc32a.dat
//********* qap.cpp *********
#include <iostream>
#include <fstream>
#include <vector>
#include "localsolver.h"
using namespace localsolver;
using namespace std;
class Qap {
public:
// Number of points
int n;
// Distance between locations
vector<vector<int> > A;
// Flow between facilites
vector<vector<lsint> > B;
// Solver.
LocalSolver localsolver;
// LS Program variables
LSExpression p;
// Objective
LSExpression obj;
// Reads instance data
void readInstance(const string& fileName){
ifstream infile;
infile.exceptions(ifstream::failbit | ifstream::badbit);
infile.open(fileName.c_str());
infile >> n;
A.resize(n);
for(int i = 0; i < n; i++){
A[i].resize(n);
for(int j = 0; j < n; j++){
infile >> A[i][j];
}
}
B.resize(n);
for(int i = 0; i < n; i++){
B[i].resize(n);
for(int j = 0; j < n; j++){
infile >> B[i][j];
}
}
}
void solve(int limit){
// Declares the optimization model.
LSModel model = localsolver.getModel();
// Permutation such that p[i] is the facility on the location i
p = model.listVar(n);
// The list must be complete
model.constraint(model.count(p) == n);
// Create B as an array to be accessed by an at operator
LSExpression arrayB = model.array();
for (int i = 0; i < n; i++) {
arrayB.addOperand(model.array(B[i].begin(), B[i].end()));
}
// Minimize the sum of product distance*flow
obj = model.sum();
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
obj += A[i][j] * model.at(arrayB, p[i], p[j]);
}
}
model.minimize(obj);
model.close();
// Parameterizes the solver.
LSPhase phase = localsolver.createPhase();
phase.setTimeLimit(limit);
localsolver.solve();
}
// Writes the solution in a file with the following format:
// - n objValue
// - permutation p
void writeSolution(const string& fileName){
ofstream outfile;
outfile.exceptions(ofstream::failbit | ofstream::badbit);
outfile.open(fileName.c_str());
outfile << n << " " << obj.getValue() << "\n";
LSCollection pCollection = p.getCollectionValue();
for (int i = 0; i < n; i++) {
outfile << pCollection.get(i) << " ";
}
outfile << endl;
}
};
int main(int argc, char** argv) {
if (argc < 2) {
cerr << "Usage: qap inputFile [outputFile] [timeLimit]" << endl;
return 1;
}
const char* instanceFile = argv[1];
const char* solFile = argc > 2 ? argv[2] : NULL;
const char* strTimeLimit = argc > 3 ? argv[3] : "300";
try {
Qap model;
model.readInstance(instanceFile);
model.solve(atoi(strTimeLimit));
if(solFile != NULL) model.writeSolution(solFile);
return 0;
} catch (const exception& e){
cerr << "Error occurred:" << e.what() << endl;
return 1;
}
}
- Compilation/Execution (Windows)
- copy %LS_HOME%\bin\*net.dll .csc Qap.cs /reference:localsolvernet.dllQap instances\esc32a.dat
/********** Qap.cs **********/
using System;
using System.IO;
using localsolver;
public class Qap : IDisposable
{
// Number of points
int n;
// Distance between locations
int[][] A;
// Flow between facilites
long[][] B;
// Solver.
LocalSolver localsolver;
// LS Program variables
LSExpression p;
// Objective
LSExpression obj;
public Qap()
{
localsolver = new LocalSolver();
}
private int readInt(string[] splittedLine, ref int lastPosRead)
{
lastPosRead++;
return int.Parse(splittedLine[lastPosRead]);
}
// Reads instance data
void ReadInstance(string fileName)
{
string text = File.ReadAllText(fileName);
string[] splitted = text.Split((char[])null, StringSplitOptions.RemoveEmptyEntries);
int lastPosRead = -1;
n = readInt(splitted, ref lastPosRead);
A = new int[n][];
for (int i = 0; i < n; i++)
{
A[i] = new int[n];
for (int j = 0; j < n; j++)
{
A[i][j] = readInt(splitted, ref lastPosRead);
}
}
B = new long[n][];
for (int i = 0; i < n; i++)
{
B[i] = new long[n];
for (int j = 0; j < n; j++)
{
B[i][j] = readInt(splitted, ref lastPosRead);
}
}
}
public void Dispose()
{
if (localsolver != null)
localsolver.Dispose();
}
void Solve(int limit)
{
// Declares the optimization model
LSModel model = localsolver.GetModel();
// Permutation such that p[i] is the facility on the location i
p = model.List(n);
// The list must be complete
model.Constraint(model.Count(p) == n);
// Create B as an array to be accessed by an at operator
LSExpression arrayB = model.Array(B);
// Minimize the sum of product distance*flow
obj = model.Sum();
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
// arrayB[a, b] is a shortcut for accessing the multi-dimensional array
// arrayB with an at operator. Same as model.At(arrayB, a, b)
obj.AddOperand(A[i][j] * arrayB[p[i], p[j]]);
}
}
model.Minimize(obj);
model.Close();
// Parameterizes the solver.
LSPhase phase = localsolver.CreatePhase();
phase.SetTimeLimit(limit);
localsolver.Solve();
}
// Writes the solution in a file with the following format:
// - n objValue
// - permutation p
void WriteSolution(string fileName)
{
using (StreamWriter output = new StreamWriter(fileName))
{
output.WriteLine(n + " " + obj.GetValue());
LSCollection pCollection = p.GetCollectionValue();
for (int i = 0; i < n; i++)
{
output.Write(pCollection.Get(i) + " ");
}
output.WriteLine();
}
}
public static void Main(string[] args)
{
if (args.Length < 1)
{
Console.WriteLine("Usage: Qap inputFile [solFile] [timeLimit]");
Environment.Exit(1);
}
string instanceFile = args[0];
string outputFile = args.Length > 1 ? args[1] : null;
string strTimeLimit = args.Length > 2 ? args[2] : "300";
using (Qap model = new Qap())
{
model.ReadInstance(instanceFile);
model.Solve(int.Parse(strTimeLimit));
if (outputFile != null)
model.WriteSolution(outputFile);
}
}
}
- Compilation / Execution (Windows)
- javac Qap.java -cp %LS_HOME%\bin\localsolver.jarjava -cp %LS_HOME%\bin\localsolver.jar;. Qap instances\esc32a.dat
- Compilation/Execution (Linux)
- javac Qap.java -cp /opt/localsolver_XXX/bin/localsolver.jarjava -cp /opt/localsolver_XXX/bin/localsolver.jar:. Qap instances/esc32a.dat
/********** Qap.java **********/
import java.util.*;
import java.io.*;
import localsolver.*;
public class Qap {
// Number of points
private int n;
// Distance between locations
private int[][] A;
// Flow between facilites
private long[][] B;
// Solver.
private LocalSolver localsolver;
// LS Program variables
private LSExpression p;
// Objective
private LSExpression obj;
// Reads instance data
private void readInstance(String fileName) throws IOException {
try(Scanner input = new Scanner(new File(fileName))) {
n = input.nextInt();
A = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
A[i][j] = input.nextInt();
}
}
B = new long[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
B[i][j] = input.nextInt();
}
}
}
}
private void solve(int limit) {
localsolver = new LocalSolver();
// Declares the optimization model
LSModel model = localsolver.getModel();
// Permutation such that p[i] is the facility on the location i
p = model.listVar(n);
// [] operator is not overloaded, so we create a LSExpression array for easier access
// of the elements of the permitation (instead of creating an at operator by hand
// everytime we want to access an element in the list)
LSExpression[] pElements = new LSExpression[n];
for (int i = 0; i < n; i++) {
pElements[i] = model.at(p, i);
}
// The list must be complete
model.constraint(model.eq(model.count(p), n));
// Create B as an array to be accessed by an at operator
LSExpression arrayB = model.array(B);
// Minimize the sum of product distance*flow
obj = model.sum();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
LSExpression prod = model.prod();
prod.addOperand(A[i][j]);
prod.addOperand(model.at(arrayB, pElements[i], pElements[j]));
obj.addOperand(prod);
}
}
model.minimize(obj);
model.close();
// Parameterizes the solver.
LSPhase phase = localsolver.createPhase();
phase.setTimeLimit(limit);
localsolver.solve();
}
// Writes the solution in a file with the following format:
// - n objValue
// - permutation p
private void writeSolution(String fileName) throws IOException {
try(PrintWriter output = new PrintWriter(fileName)) {
output.println(n + " " + obj.getValue());
LSCollection pCollection = p.getCollectionValue();
for (int i = 0; i < n; i++)
output.print(pCollection.get(i) + " ");
output.println();
}
}
public static void main(String[] args) {
if (args.length < 1) {
System.out.println("Usage: java Qap inputFile [outputFile] [timeLimit]");
System.exit(1);
}
String instanceFile = args[0];
String outputFile = args.length > 1 ? args[1] : null;
String strTimeLimit = args.length > 2 ? args[2] : "300";
try {
Qap model = new Qap();
model.readInstance(instanceFile);
model.solve(Integer.parseInt(strTimeLimit));
if (outputFile != null) {
model.writeSolution(outputFile);
}
} catch(Exception ex) {
System.err.println(ex);
ex.printStackTrace();
System.exit(1);
}
}
}
