Bin packing¶
Principles learned¶
- Create a set decision variable
- Use a lambda expression to compute a sum on a set
- Specify a threshold to stop the search after a target is reached
Problem¶
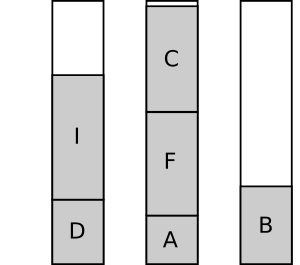
In the bin packing problem, a number of items with known weights must be assigned to bins with uniform capacity. The objective is to minimize the number of bins used such that all items are placed. It is a typical example of an NP-hard problem.
Download the exampleData¶
The instances provided are the Falkenauer instances from the BPPLIB. The format of the data files is as follows:
- First line: number of items
- Second line: capacity of a bin
- The weight for each item
Program¶
The model implemented here makes use of set variables. For each bin we define a set which describes the items assigned to that bin. Those sets are constrained to form a partition, which means that an item must be assigned to exactly one bin.
For each bin, the combined weight of the items must be smaller than its capacity. This weight is computed directly using the sum operator on the set: we define a function that takes an item index and returns the associated weight. See our documentation on this topic for details.
The model computes simple lower and upper bounds on the optimal number
of bins. It only defines nbMaxBins set variables, and uses
lsObjectiveThreshold to stop the search if a solution with nbMinBins
bins is reached.
- Execution:
- localsolver bin_packing.lsp inFileName=instances/t60_00.txt [lsTimeLimit=] [solFileName=]
/********** bin_packing.lsp **********/
use io;
/* Reads instance data. */
function input() {
local usage = "Usage: localsolver bin_packing.lsp "
+ "inFileName=inputFile [lsTimeLimit=timeLimit]";
if (inFileName == nil) throw usage;
local inFile = io.openRead(inFileName);
nbItems = inFile.readInt();
binCapacity = inFile.readInt();
itemWeights[i in 0..nbItems-1] = inFile.readInt();
nbMinBins = ceil(sum[i in 0..nbItems-1](itemWeights[i])/binCapacity);
nbMaxBins = min(nbItems, 2 * nbMinBins);
}
/* Declares the optimization model. */
function model() {
// Set decisions: bins[k] represents the items in bin k
bins[k in 0..nbMaxBins-1] <- set(nbItems);
// Each item must be in one bin and one bin only
constraint partition[k in 0..nbMaxBins-1](bins[k]);
for [k in 0..nbMaxBins-1] {
// Weight constraint for each bin
binWeights[k] <- sum(bins[k], i => itemWeights[i]);
constraint binWeights[k] <= binCapacity;
// Bin k is used if at least one item is in it
binsUsed[k] <- (count(bins[k]) > 0);
}
// Count the used bins
totalBinsUsed <- sum[k in 0..nbMaxBins-1](binsUsed[k]);
// Minimize the number of used bins
minimize totalBinsUsed;
}
/* Parameterizes the solver. */
function param() {
if (lsTimeLimit == nil) lsTimeLimit = 20;
if (lsNbThreads == nil) lsNbThreads = 1;
if (lsTimeBetweenDisplays == nil) lsTimeBetweenDisplays = 1;
// Stop the search if the lower threshold is reached
lsObjectiveThreshold = nbMinBins;
}
function output() {
for[k in 0..nbMaxBins-1] {
if (count(bins[k].value) > 0) {
print("Bin weight: ", binWeights[k].value, " | Items: ");
for[e in bins[k].value]
print(e + " ");
println();
}
}
}
- Execution (Windows)
- set PYTHONPATH=%LS_HOME%\bin\pythonpython bin_packing.py instances\t60_00.txt
- Execution (Linux)
- export PYTHONPATH=/opt/localsolver_10_5/bin/pythonpython bin_packing.py instances/t60_00.txt
########## bin_packing.py ##########
import localsolver
import sys
import math
if len(sys.argv) < 2:
print("Usage: python bin_packing.py inputFile [outputFile] [timeLimit]")
sys.exit(1)
def read_integers(filename):
with open(filename) as f:
return [int(elem) for elem in f.read().split()]
with localsolver.LocalSolver() as ls:
# Reads instance data
file_it = iter(read_integers(sys.argv[1]))
nb_items = int(next(file_it))
bin_capacity = int(next(file_it))
item_weights = [int(next(file_it)) for i in range(nb_items)]
nb_min_bins = int(math.ceil(sum(item_weights)/float(bin_capacity)))
nb_max_bins = min(nb_items, 2 * nb_min_bins)
# Declares the optimization model
model = ls.model
# Set decisions: bin[k] represents the items in bin k
bins = [model.set(nb_items) for k in range(nb_max_bins)]
# Each item must be in one bin and one bin only
model.constraint(model.partition(bins))
weight_array = model.array(item_weights)
weight_selector = model.lambda_function(lambda i: weight_array[i])
# Weight constraint for each bin
bin_weights = [model.sum(b, weight_selector) for b in bins]
for w in bin_weights:
model.constraint(w <= bin_capacity)
# Bin k is used if at least one item is in it
bins_used = [model.count(b) > 0 for b in bins]
# Count the used bins
total_bins_used = model.sum(bins_used)
# Minimize the number of used bins
model.minimize(total_bins_used)
model.close()
# Parameterizes the solver
if len(sys.argv) >= 4: ls.param.time_limit = int(sys.argv[3])
else: ls.param.time_limit = 5
# Stop the search if the lower threshold is reached
ls.param.set_objective_threshold(0, nb_min_bins)
ls.solve()
# Writes the solution in a file
if len(sys.argv) >= 3:
with open(sys.argv[2], 'w') as f:
for k in range(nb_max_bins):
if bins_used[k].value:
f.write("Bin weight: %d | Items: " % bin_weights[k].value)
for e in bins[k].value:
f.write("%d " % e)
f.write("\n")
- Compilation / Execution (Windows)
- cl /EHsc bin_packing.cpp -I%LS_HOME%\include /link %LS_HOME%\bin\localsolver105.libbin_packing instances\t60_00.txt
- Compilation / Execution (Linux)
- g++ bin_packing.cpp -I/opt/localsolver_10_5/include -llocalsolver105 -lpthread -o bin_packing./bin_packing instances/t60_00.txt
/********** bin_packing.cpp **********/
#include <iostream>
#include <fstream>
#include <vector>
#include <numeric>
#include <cmath>
#include "localsolver.h"
using namespace localsolver;
using namespace std;
class BinPacking {
private:
// Number of items
int nbItems;
// Capacity of each bin
int binCapacity;
// Maximum number of bins
int nbMaxBins;
// Minimum number of bins
int nbMinBins;
// Weight of each item
std::vector<lsint> itemWeights;
// LocalSolver
LocalSolver localsolver;
// Decision variables
std::vector<LSExpression> bins;
// Weight of each bin in the solution
std::vector<LSExpression> binWeights;
// Whether the bin is used in the solution
std::vector<LSExpression> binsUsed;
// Objective
LSExpression totalBinsUsed;
public:
// Reads instance data.
void readInstance(const string& fileName) {
ifstream infile;
infile.exceptions(ifstream::failbit | ifstream::badbit);
infile.open(fileName.c_str());
infile >> nbItems;
infile >> binCapacity;
itemWeights.resize(nbItems);
for (int i = 0; i < nbItems; ++i) {
infile >> itemWeights[i];
}
nbMinBins = ceil(accumulate(itemWeights.begin(), itemWeights.end(), 0.0) / binCapacity);
nbMaxBins = min(2 * nbMinBins, nbItems);
}
void solve(int limit) {
// Declares the optimization model.
LSModel model = localsolver.getModel();
bins.resize(nbMaxBins);
binWeights.resize(nbMaxBins);
binsUsed.resize(nbMaxBins);
// Set decisions: bins[k] represents the items in bin k
for (int k = 0; k < nbMaxBins; ++k) {
bins[k] = model.setVar(nbItems);
}
// Each item must be in one bin and one bin only
model.constraint(model.partition(bins.begin(), bins.end()));
// Create an array and a function to retrieve the item's weight
LSExpression weightArray = model.array(itemWeights.begin(), itemWeights.end());
LSExpression weightSelector = model.createLambdaFunction([&](LSExpression i) { return weightArray[i]; });
for (int k = 0; k < nbMaxBins; ++k) {
// Weight constraint for each bin
binWeights[k] = model.sum(bins[k], weightSelector);
model.constraint(binWeights[k] <= binCapacity);
// Bin k is used if at least one item is in it
binsUsed[k] = model.count(bins[k]) > 0;
}
// Count the used bins
totalBinsUsed = model.sum(binsUsed.begin(), binsUsed.end());
// Minimize the number of used bins
model.minimize(totalBinsUsed);
model.close();
// Parameterizes the solver.
localsolver.getParam().setTimeLimit(limit);
// Stop the search if the lower threshold is reached
localsolver.getParam().setObjectiveThreshold(0, (lsint) nbMinBins);
localsolver.solve();
}
// Writes the solution in a file
void writeSolution(const string& fileName) {
ofstream outfile;
outfile.exceptions(ofstream::failbit | ofstream::badbit);
outfile.open(fileName.c_str());
for (int k = 0; k < nbMaxBins; ++k) {
if (binsUsed[k].getValue()) {
outfile << "Bin weight: " << binWeights[k].getValue() << " | Items: ";
LSCollection binCollection = bins[k].getCollectionValue();
for (int i = 0; i < binCollection.count(); ++i) {
outfile << binCollection[i] << " ";
}
outfile << endl;
}
}
}
};
int main(int argc, char** argv) {
if (argc < 2) {
cerr << "Usage: bin_packing inputFile [outputFile] [timeLimit]" << endl;
return 1;
}
const char* instanceFile = argv[1];
const char* solFile = argc > 2 ? argv[2] : NULL;
const char* strTimeLimit = argc > 3 ? argv[3] : "5";
try {
BinPacking model;
model.readInstance(instanceFile);
model.solve(atoi(strTimeLimit));
if (solFile != NULL) model.writeSolution(solFile);
return 0;
} catch (const exception& e) {
cerr << "An error occurred: " << e.what() << endl;
return 1;
}
}
- Compilation / Execution (Windows)
- copy %LS_HOME%\bin\localsolvernet.dll .csc BinPacking.cs /reference:localsolvernet.dllBinPacking instances\t60_00.txt
/********** BinPacking.cs **********/
using System;
using System.IO;
using System.Linq;
using localsolver;
public class BinPacking : IDisposable
{
// Number of items
int nbItems;
// Capacity of each bin
int binCapacity;
// Maximum number of bins
int nbMaxBins;
// Minimum number of bins
int nbMinBins;
// Weight of each item
long[] itemWeights;
// LocalSolver
LocalSolver localsolver;
// Decision variables
LSExpression[] bins;
// Weight of each bin in the solution
LSExpression[] binWeights;
// Whether the bin is used in the solution
LSExpression[] binsUsed;
// Objective
LSExpression totalBinsUsed;
public BinPacking()
{
localsolver = new LocalSolver();
}
// Reads instance data.
void ReadInstance(string fileName)
{
using (StreamReader input = new StreamReader(fileName))
{
nbItems = int.Parse(input.ReadLine());
binCapacity = int.Parse(input.ReadLine());
itemWeights = new long[nbItems];
for (int i = 0; i < nbItems; i++) {
itemWeights[i] = int.Parse(input.ReadLine());
}
nbMinBins = (int) Math.Ceiling((double) itemWeights.Sum() / binCapacity);
nbMaxBins = Math.Min(2 * nbMinBins, nbItems);
}
}
public void Dispose()
{
if (localsolver != null)
localsolver.Dispose();
}
void Solve(int limit)
{
// Declares the optimization model.
LSModel model = localsolver.GetModel();
bins = new LSExpression[nbMaxBins];
binWeights = new LSExpression[nbMaxBins];
binsUsed = new LSExpression[nbMaxBins];
// Set decisions: bin[k] represents the items in bin k
for (int k = 0; k < nbMaxBins; ++k) {
bins[k] = model.Set(nbItems);
}
// Each item must be in one bin and one bin only
model.Constraint(model.Partition(bins));
// Create an array and a function to retrieve the item's weight
LSExpression weightArray = model.Array(itemWeights);
LSExpression weightSelector = model.LambdaFunction(i => weightArray[i]);
for (int k = 0; k < nbMaxBins; ++k) {
// Weight constraint for each bin
binWeights[k] = model.Sum(bins[k], weightSelector);
model.Constraint(binWeights[k] <= binCapacity);
// Bin k is used if at least one item is in it
binsUsed[k] = model.Count(bins[k]) > 0;
}
// Count the used bins
totalBinsUsed = model.Sum(binsUsed);
// Minimize the number of used bins
model.Minimize(totalBinsUsed);
model.Close();
// Parameterizes the solver.
localsolver.GetParam().SetTimeLimit(limit);
// Stop the search if the lower threshold is reached
localsolver.GetParam().SetObjectiveThreshold(0, nbMinBins);
localsolver.Solve();
}
// Writes the solution in a file
void WriteSolution(string fileName)
{
using (StreamWriter output = new StreamWriter(fileName))
{
for (int k = 0; k < nbMaxBins; ++k) {
if (binsUsed[k].GetValue() != 0) {
output.Write("Bin weight: " + binWeights[k].GetValue() + " | Items: ");
LSCollection binCollection = bins[k].GetCollectionValue();
for (int i = 0; i < binCollection.Count(); ++i) {
output.Write(binCollection[i] + " ");
}
output.WriteLine();
}
}
}
}
public static void Main(string[] args)
{
if (args.Length < 1)
{
Console.WriteLine("Usage: BinPacking inputFile [solFile] [timeLimit]");
Environment.Exit(1);
}
string instanceFile = args[0];
string outputFile = args.Length > 1 ? args[1] : null;
string strTimeLimit = args.Length > 2 ? args[2] : "5";
using (BinPacking model = new BinPacking())
{
model.ReadInstance(instanceFile);
model.Solve(int.Parse(strTimeLimit));
if (outputFile != null)
model.WriteSolution(outputFile);
}
}
}
- Compilation / Execution (Windows)
- javac BinPacking.java -cp %LS_HOME%\bin\localsolver.jarjava -cp %LS_HOME%\bin\localsolver.jar;. BinPacking instances\t60_00.txt
- Compilation / Execution (Linux)
- javac BinPacking.java -cp /opt/localsolver_10_5/bin/localsolver.jarjava -cp /opt/localsolver_10_5/bin/localsolver.jar:. BinPacking instances/t60_00.txt
/********** BinPacking.java **********/
import java.util.*;
import java.io.*;
import localsolver.*;
public class BinPacking {
// Number of items
private int nbItems;
// Capacity of each bin
private int binCapacity;
// Maximum number of bins
private int nbMaxBins;
// Minimum number of bins
private int nbMinBins;
// Weight of each item
private long[] itemWeights;
// LocalSolver
private final LocalSolver localsolver;
// Decision variables
private LSExpression[] bins;
// Weight of each bin in the solution
private LSExpression[] binWeights;
// Whether the bin is used in the solution
private LSExpression[] binsUsed;
// Objective
private LSExpression totalBinsUsed;
private BinPacking(LocalSolver localsolver) {
this.localsolver = localsolver;
}
// Reads instance data.
private void readInstance(String fileName) throws IOException {
try (Scanner input = new Scanner(new File(fileName))) {
nbItems = input.nextInt();
binCapacity = input.nextInt();
itemWeights = new long[nbItems];
for (int i = 0; i < nbItems; i++) {
itemWeights[i] = input.nextInt();
}
long sumWeights = 0;
for (int i = 0; i < nbItems; i++) {
sumWeights += itemWeights[i];
}
nbMinBins = (int) Math.ceil((double) sumWeights / binCapacity);
nbMaxBins = Math.min(2 * nbMinBins, nbItems);
}
}
private void solve(int limit) {
// Declares the optimization model.
LSModel model = localsolver.getModel();
bins = new LSExpression[nbMaxBins];
binWeights = new LSExpression[nbMaxBins];
binsUsed = new LSExpression[nbMaxBins];
// Set decisions: bins[k] represents the items in bin k
for (int k = 0; k < nbMaxBins; ++k) {
bins[k] = model.setVar(nbItems);
}
// Each item must be in one bin and one bin only
model.constraint(model.partition(bins));
// Create an array and a lambda function to retrieve the item's weight
LSExpression weightArray = model.array(itemWeights);
LSExpression weightSelector = model.lambdaFunction(i -> model.at(weightArray, i));
for (int k = 0; k < nbMaxBins; ++k) {
// Weight constraint for each bin
binWeights[k] = model.sum(bins[k], weightSelector);
model.constraint(model.leq(binWeights[k], binCapacity));
// Bin k is used if at least one item is in it
binsUsed[k] = model.gt(model.count(bins[k]), 0);
}
// Count the used bins
totalBinsUsed = model.sum(binsUsed);
// Minimize the number of used bins
model.minimize(totalBinsUsed);
model.close();
// Parameterizes the solver.
localsolver.getParam().setTimeLimit(limit);
// Stop the search if the lower threshold is reached
localsolver.getParam().setObjectiveThreshold(0, nbMinBins);
localsolver.solve();
}
// Writes the solution in a file
private void writeSolution(String fileName) throws IOException {
try (PrintWriter output = new PrintWriter(fileName)) {
for (int k = 0; k < nbMaxBins; ++k) {
if (binsUsed[k].getValue() != 0) {
output.print("Bin weight: " + binWeights[k].getValue() + " | Items: ");
LSCollection binCollection = bins[k].getCollectionValue();
for (int i = 0; i < binCollection.count(); ++i) {
output.print(binCollection.get(i) + " ");
}
output.println();
}
}
}
}
public static void main(String[] args) {
if (args.length < 1) {
System.err.println("Usage: java BinPacking inputFile [outputFile] [timeLimit]");
System.exit(1);
}
String instanceFile = args[0];
String outputFile = args.length > 1 ? args[1] : null;
String strTimeLimit = args.length > 2 ? args[2] : "20";
try (LocalSolver localsolver = new LocalSolver()) {
BinPacking model = new BinPacking(localsolver);
model.readInstance(instanceFile);
model.solve(Integer.parseInt(strTimeLimit));
if (outputFile != null) {
model.writeSolution(outputFile);
}
} catch (Exception ex) {
System.err.println(ex);
ex.printStackTrace();
System.exit(1);
}
}
}
