Hexaly on very large-scale instances of the Capacitated Vehicle Routing Problem (CVRP)
The 12th DIMACS Implementation Challenge, a renowned mathematical optimization competition, focused on solving Vehicle Routing Problems (VRP). The goal of such an event, bringing together the best experts and researchers in the field, is to have a clear picture of the state of the art on a given class of problems, like VRP, by practically comparing the best algorithms from the literature with scientific rigor. Capacitated Vehicle Routing Problem (CVRP) was one of the problems addressed. During the challenge, some of the best known solutions were improved by dedicated algorithms on the largest CVRP instances, involving several thousand points to serve.
In this post, we analyze the performance and scalability of Hexaly, a general-purpose optimization solver, on the biggest instances used during the challenge, for which the state of the art (SOTA) was improved. We consider the dataset introduced in 2017 by Arnold, Gendreau, and Sörensen. The given problems, with sizes from 3,000 to 30,000 points to serve, have been tested with Hexaly 13.0 using the CVRP model directly available from Hexaly’s Example Tour. As in the challenge, the objective is to minimize the total distance without restrictions on the number of used trucks. We performed this experiment on a server equipped with an AMD Ryzen 7 7700 processor (8 cores, 3.8GHz, 8MB cache) and 32GB RAM.
Hexaly reaches a 4.4% average gap to the best known solutions in the research in 1 minute of running time on these very large-scale CVRP instances. The table below presents the gap, expressed in %, between the solutions found by Hexaly and the SOTA solutions as reported here. Note that the SOTA solutions are computed using dedicated algorithms, using arbitrary long running times on specific hardware.
| Hexaly 13.0 | ||||
|---|---|---|---|---|
| Instance | Size | 1 min | 10 min | 1 hour |
| Leuven1 | 3,000 | 1.7 | 1.3 | 1.1 |
| Leuven2 | 4,000 | 4.5 | 3.5 | 3.1 |
| Antwerp1 | 6,000 | 2.3 | 1.7 | 1.4 |
| Antwerp2 | 7,000 | 5.8 | 4.1 | 3.4 |
| Ghent1 | 10,000 | 4.0 | 2.36 | 1.5 |
| Ghent2 | 11,000 | 5.9 | 4.4 | 3.6 |
| Brussels1 | 15,000 | 3.8 | 2.8 | 2.1 |
| Brussels2 | 16,000 | 6.7 | 5.1 | 4.0 |
| Flanders1 | 20,000 | 3.0 | 2.2 | 1.6 |
| Flanders2 | 30,000 | 6.6 | 5.2 | 4.3 |
In 1 minute of running time, Hexaly finds solutions with a 4.4% average gap over the 10 instances. On the huge 30,000-point instance, Hexaly delivers a solution with a 6.6% gap. Within 1 hour of computation time, the worst gap observed decreases below 5%, even for the largest instance involving 30,000 points. The average gap over the whole dataset is reduced to 3.3% within 10 minutes and 2.6 % within 1 hour.
These massive CVRP instances are out of reach for traditional Mixed-Integer Linear Programming (MILP) solvers with a direct formulation. You can find a benchmark on CVRP between Hexaly and Gurobi on smaller instances here.
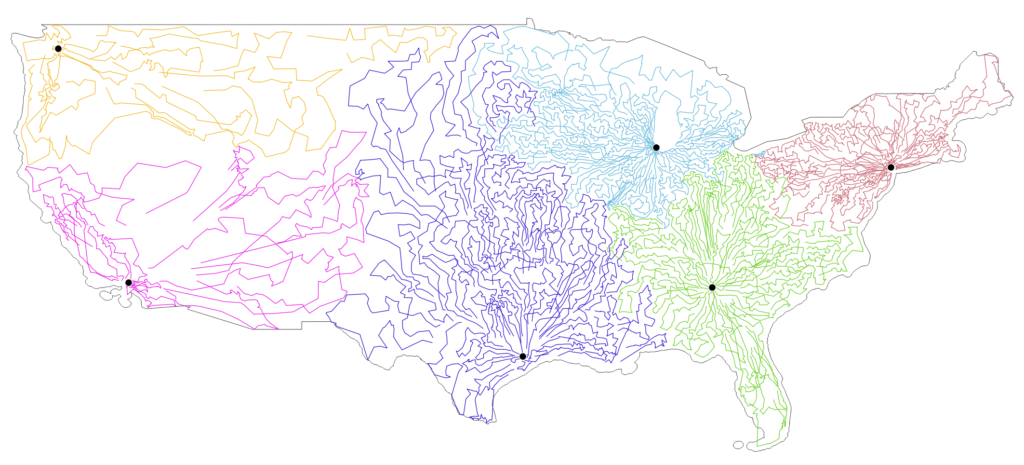
To illustrate the quality of the solution obtained by Hexaly on very large-scale instances, we generated a Multi-Depot Capacitated Vehicle Routing Problem with 14,000 points to serve, corresponding to United States cities with at least 500 inhabitants and 6 depots located among the largest cities in the country. The map below shows the solution obtained within 10 minutes of running time. For clarity, the tours have been partially drawn to avoid too much color concentration around the depot. While solely resulting from the global optimization of routes, the clustering induced by the deliveries around the depots is almost perfect.
In our Example Tour, you can find the complete model for the Capacitated Vehicle Routing Problem (CVRP), as well as for many other Vehicle Routing problems like Capacitated Vehicle Routing Problem with Time Windows (CVRPTW) or Pickup and Delivery Problem with Time Windows (PDPTW). Code snippets are given for common programming languages like Python, Java, C#, and C++.
Ready to start?
Discover the ease of use and performance of Hexaly through a free 1-month trial.

